Vectors in Particle Physics

---

Conservation Laws - Data Analysis Using Graphs - Histograms - Units or Vectors in Particle Physics

---

Naming and Defining
Vectors have: Length Direction velocity: 30 m/s southeast momentum: 5 kg m/s 30oE of N displacement: 8 m east Scalars are just numerical; they have no direction. mass: 4 kg kinetic energy: 27 Joules time: 15 s	Is force a scalar or a vector? Is age a scalar or a vector?
You show a vector by bold font or an arrow over its symbol.
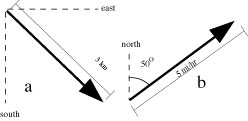
You can name a vector by its length and direction: a. 3 km, southeast. b. 5 mi/hr at 50o east of north.
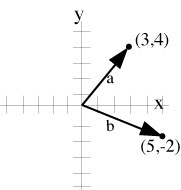
Or, you can name a vector by the x- and y-coordinates of its endpoints, if its tail is at the origin. a. (3,4) b. (5,-2).
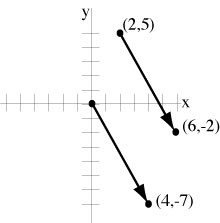
You can move a vector parallel to itself. The vector from (2,5) to (6,-2) is the same as the one from the origin to (4,-7)
Using trig, you can switch from one description to the other. A force of 8 Newtons is applied 30o above the horizontal. In the triangle, the cosine of 30o is x/8. So the x-component is (8N) x cos 30o. Similarly, the y-component is (8N) x sin 30o.
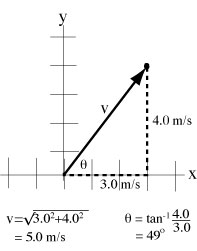
If the vector coordinates are (3.0,4.0): the length (by Pythagorean Theorem) is the square root of (3.02 + 4.02) = 5.0. The direction is determined by the tangent of the angle = (4.0/3.0).
Find the x and y components of the momentum, p = 5.0 kg m/s at 130o.
Find the length and direction for the displacement vector from (3.0 meters,4.0 m) to (-1.0 m,-2.0 m).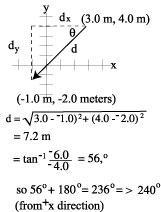
Adding Vectors Graphically
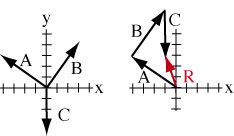
Add vectors by drawing them head to tail. That is, each vector starts where the last one stopped. The sum (resultant) is the vector from the tail of the first to the head of the last vector. Measure its length and direction to the same scale.
Adding Vectors Algebraically
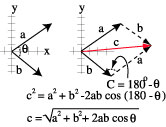
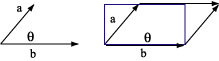
To add only two vectors, use the law of cosines. Draw the vectors head to tail. Then the resultant is the other side of the triangle. c2 = a2 + b2 - 2 ab cos C, where a, b, and c are sides and angle C is opposite side c.
To add several vectors, add their x-components and their y-components. The length is the square root of (ΣSx)2 + (Σy)2) where x and y are the total x and y components. The direction is tan-1 of Σy/Σx.
Multiplying Vectors - Dot Product
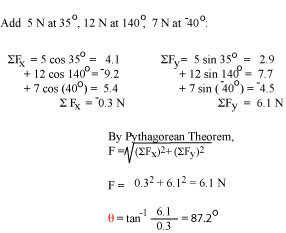The dot product of two vectors gives a scalar answer. To find the dot product, you must know the length of each vector and the angle between them (θ): A.B = ABcosθ For example, work is a scalar product of the force vector and the distance vector. W = F . d = Fdcosθ, or, W = Fx d, where Fx is the component of F in the direction of d.	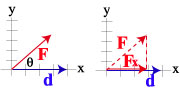F and d are not drawn to the same scale. The illustration is meant to help you find the component of F that is in the direction of d
Multiplying Vectors - Cross Product
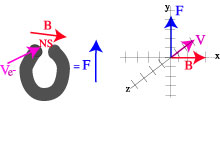
The cross product of two vectors gives a vector answer. The direction of that answer is perpendicular to the plane that contains A & B. The length of the answer comes from: |A x B| = ABsinθ For example, a charged particle moving in a magnetic field feels a force: F = qv x B The charge of the particle is q. The vector velocity of the particle is v. The vector magnetic field is B. The resulting force, F, is also a vector and is perpendicular to to the vB plane.
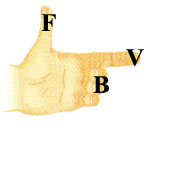
There are many memory tricks for figuring out the direction of the resulting vector. Here is one. Use the left hand for negatively charged particles. Use right hand for positively charged particles. The forefinger indicates the direction of the velocity. The middle finger indicates the direction of the B field. The two fingers comprise the plane which contains v and B. The thumb is perpendicular to this plane and indicates the direction of the force.