Histograms: Construction, Analysis and Understanding
Conservation Laws - Data Analysis Using Graphs - Histograms - Units or Vectors in Particle Physics
What is a Histogram?
A histogram is "a representation of a frequency distribution by means of rectangles whose widths represent class intervals and whose areas are proportional to the corresponding frequencies."
Online Webster's Dictionary

Sounds complicated . . . but the concept really is pretty simple. We graph groups of numbers according to how often they appear. Thus if we have the set {1,2,2,3,3,3,3,4,4,5,6}, we can graph them like this:

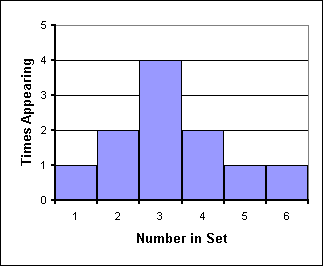
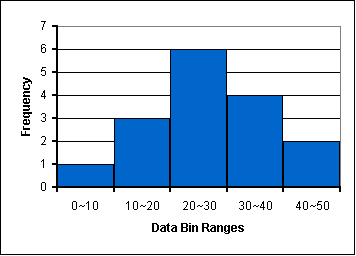
This graph is pretty easy to make and gives us some useful data about the set. For example, the graph peaks at 3, which is also the median and the mode of the set. The mean of the set is 3.27—also not far from the peak. The shape of the graph gives us an idea of how the numbers in the set are distributed about the mean; the distribution of this graph is wide compared to size of the peak, indicating that values in the set are only loosely bunched around the mean.

 

 

How is a Real Histogram Made?
The example above is a little too simple. In most real data sets almost all numbers will be unique. Consider the set {3, 11, 12, 19, 22, 23, 24, 25, 27, 29, 35, 36, 37, 45, 49}. A graph which shows how many ones, how many twos, how many threes, etc. would be meaningless. Instead, we bin the data into convenient ranges. In this case, with a bin width of 10, we can easily group the data as below.

Note: Changing the size of the bin changes the apprearance of the graph and the conclusions you may draw from it. The Shodor histogram activity allows you to change the bin size for a data set and the impact on the curve.


Data Range Frequency
0-10 1
10-20 3
20-30 6
30-40 4
40-50 2

Note that the median is 25 and that there is no mode; the mean is 26.5.

How Shall We Look at Histograms?
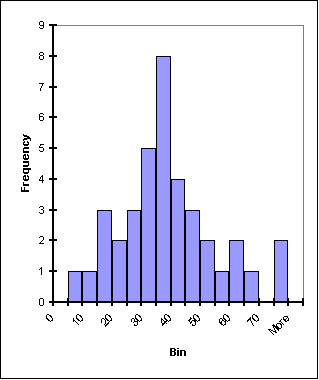
Of course, part of the power of histograms is that they allow us to analyze extremely large datasets by reducing them to a single graph that can show primary, secondary and tertiary peaks in data as well as give a visual representation of the statistical significance of those peaks. To get an idea, look at these three histograms:

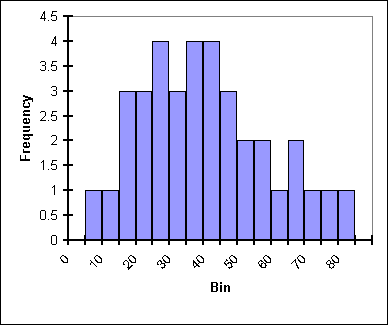This plot represents data with a well-defined peak that is close in value to the median and the mean. While there are "outlyers," they are of relatively low frequency. Thus it can be said that deviations in this data group from the mean are of low frequency. If this were a mass plot in particle physics, we'd say the mass is understood with good precision. In this plot the peak is still fairly close to the median and the mean, but it is much less defined. It is harder to tell from the plot what the exact location of the peak is. There are almost as many values close to the peak as at the peak itself and outlyers are frequent. As a particle physics mass plot, this gives an imprecise and uncertain mass of a particle.
Where are the median and the mean? It is hard to tell; it also may not be relevant. There are two peaks in this plot: a taller primary peak as well as a shorter secondary peak. This could indicate either very poor definition of one signal in the data or, more likely, two signals. In particle physics, this could show two separate particles or, as is often the case, a large signal with "background" particles and a smaller signal (sometimes very small), called a "bump," which shows the actual particle under study.
Resources
Project Contact: Ken Cecire
Web Maintainer: qnet-webmaster@fnal.gov
Last Update: March 22, 2002