|
Vectors in Particle Physics |
 |
Conservation Laws - Data Analysis Using Graphs - Histograms - Units or Vectors in Particle Physics
|
Naming and Defining Adding Graphically Adding Algebraically |
Multiplying - Dot Product Multiplying - Cross Product |
|
| |||||||||||||||||||
Scalars are just numerical; they have no direction.
|
Is force a scalar or a vector? Is age a scalar or a vector? | ||||||||||||||||||
You show a vector by bold font or an arrow over its symbol. |
 | ||||||||||||||||||
|
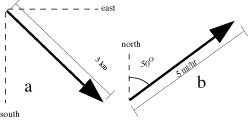
You can name a vector by its length and direction:
a. 3 km, southeast. |
 | ||||||||||||||||||
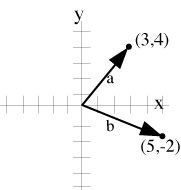
| Or, you can name a vector by the x- and y-coordinates of its endpoints, if its tail is at the origin. a. (3,4) b. (5,-2). |
 | ||||||||||||||||||
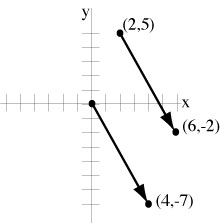
| You can move a vector parallel to itself. The vector from (2,5) to (6,-2) is the same as the one from the origin to (4,-7) |
 | ||||||||||||||||||
| Using trig, you can switch from one description to the other. A force of 8 Newtons is applied 30o above the horizontal.
In the triangle, the cosine of 30o is x/8. |
 | ||||||||||||||||||
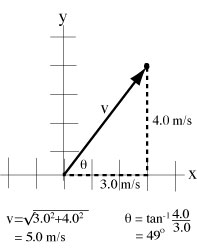
| If the vector coordinates are (3.0,4.0): the length (by Pythagorean Theorem) is the square root of (3.02 + 4.02) = 5.0. The direction is determined by the tangent of the angle = (4.0/3.0).
|
 | ||||||||||||||||||
| Find the x and y components of the momentum, p = 5.0 kg m/s at 130o. |  | ||||||||||||||||||
| Find the length and direction for the displacement vector from (3.0 meters,4.0 m) to (-1.0 m,-2.0 m). | 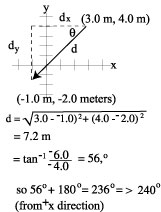 | ||||||||||||||||||
| Adding Vectors Graphically | |||||||||||||||||||
|
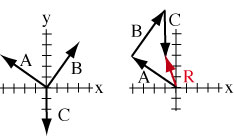
Add vectors by drawing them head to tail. That is, each vector starts where the last one stopped.
The sum (resultant) is the vector from the tail of the first to the head of the last vector. Measure its length and direction to the same scale. |
 | ||||||||||||||||||
| | |||||||||||||||||||
|
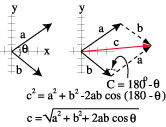
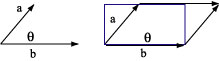
To add only two vectors, use the law of cosines. Draw the vectors head to tail.
Then the resultant is the other side of the triangle.
c2 = a2 + b2 - 2 ab
cos C, |
 | ||||||||||||||||||
| To add several vectors, add their x-components and their y-components.
The length is the square root of (ΣSx)2 +
(Σy)2) where x and y are the total x and y components. |
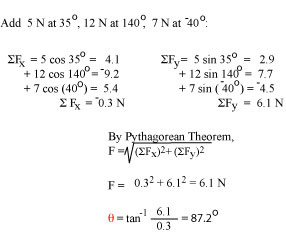 | ||||||||||||||||||
|
The dot product of two vectors gives a scalar answer. To find the dot product, you must know the length of each vector and the angle between them (θ): A.B = ABcosθ For example, work is a scalar product of the force vector and the distance vector. W = F . d = Fdcosθ,
or, W = Fx d, where Fx is the component of F in the direction of d. | 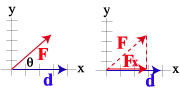 F and d are not drawn to the same scale. The illustration is meant to help you find the component of F that is in the direction of d | ||||||||||||||||||
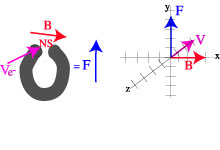
| The cross product of two vectors
gives a vector answer. The direction of that answer is perpendicular to the plane that contains A & B. The length of the answer comes from: |A x B| = ABsinθ For example, a charged particle moving in a magnetic field feels a force: F = qv x B
The charge of the particle is q. |
|
||||||||||||||||||
| There are many memory tricks for figuring out the direction of the resulting vector. Here is one. Use the left hand for negatively charged particles. Use right hand for positively charged particles.
The forefinger indicates the direction of the velocity. |
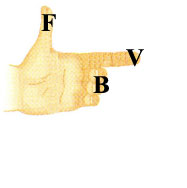 | ||||||||||||||||||