Cosmic Microwave Background
One of the predictions that the Big Bang theory leads to, concerns some left over pieces that could tell us the temperature of the universe.. IF we believe that the Big Bang is how the universe began, then theorists predict that we should see a remnant microwave background. It is microwave because that is the area of the spectrum in which it is found. When we look out into space with our bare eyes, we see bright objects and a whole lot of "empty" space. However, if we examine the sky with a radio telescope, we see an almost perfect blackbody spectrum in the microwave spectrum. What is a blackbody and why is it radiating? How did we find the Cosmic Microwave Background? And can we fit a curve to the data taken for the Cosmic Microwave Background?
Spectral Analysis
A visible spectrum is a combination of the different ranges of colors in light. At first scientists only studied visible white light. When this light passes through a prism, it separates into different frequencies and shows a rainbow of colors. Scientists realized that white light must be made up of all the different colors of light. A spectrum graph is a graph of wavelength (x-axis) versus frequency (y-axis). In order to take the spectrum of an object you need a tool called a spectrometer. The spectrometer takes the visible light and separates it into its separate frequencies and graphs it. A very nice spectrometer tool comes from Vernier, is called the SpectroVis, and works very well with the Vernier Labquest. A link to the Vernier website is below.
We can take spectra from lightbulbs, the sun, even each other if we have a sensitive enough spectrometer. However, astronomers find it very useful to take spectral data of objects in the night sky. They can tell many things about the objects just from their spectra. In the Hubble Diagram exercise you looked at magnitude and redshift. Both of these values can come from the spectrum of a galaxy. So what can the shape of a spectrum say about an object?
Blackbody Radiation
A blackbody is an object that absorbs all of the electromagnetic radiation going at it. Since nothing is reflected or passes through, a blackbody often appears "dark" to the naked eye. However, a blackbody is always emitting a spectrum that turns out is extremely temperature dependent. This means that a really hot object will emit a spectrum that is shaped the same but on a different scale than a really cold object. A blackbody spectrum has a specific curve that is extremely characteristic of that blackbody. The general shape of a blackbody spectrum is seen below.
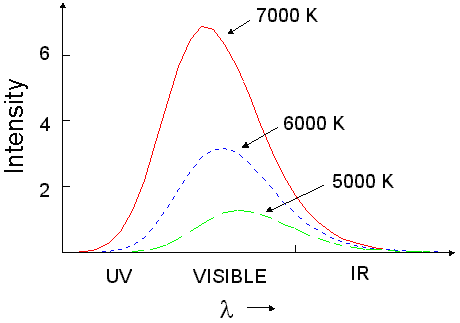
The spectral graph of a blackbody shows wavelength on the x-axis, and intensity on the y-axis. As you can see, the hotter the object, the larger the curve. Temperature is measured in Kelvin degrees. 1 degree Kelvin is equal to 273 degrees celcius. So a temperature of 7000 degrees Kelvin is pretty hot.
Excel Sheet Activity Directions
- The "Constants" sheet has three important values in it: Planck's constants, the speed of light, and Boltzman's constant. We need to use these in all the equations. Don't change any of these values!
- The "Incandescent Light Bulb" sheet has the spectrum of an ordinary incandescent light bulb. The temperature of the black body curve is set to 1000 degrees Kelvin intially. Is the bulb hotter or colder than that? Change the temperature of the black body until you get a "good enough" fit, within a few hundred degrees.
- Look at this web page for examples of some non-thermal spectra. Would you try to fit a black body spectrum to any of these?
- Now take data of some things in or near the room that may (or may not) be a black body. Check out this page for directions for working the Vernier SpectroVis. Make copies of the "Incandescent Light Bulb" sheet and put your own data there. Who in the class can find the hottest (or coldest) black body? Do different people measure the same temperature for the same object?
- The "SMARTS plots" show a standard solar spectrum from the Renewable Resource Data Center. The three versions of the spectra are for sunlight above the Earth's atmosphere (what astonomers care about), and inside the atmosphere directly from the disk of the Sun, and excluding direct light from the Sun, what you care about when you are installing solar panels. The "SMARST2 Solar Spectrum" sheet has the data with a fit to a black body. Is 1000 degrees too hot or too cold? What temperature (with a few hundred degrees) describes the sun? Is this the temperature in the middle or on the surface of the Sun? Is this hotter or colder than the light bulb?
- "BD17" is similar, for a star we use to calibrate flux in the Sloan Digital Sky Survey. BD17 is a familiar name BD17+4708. Again, the temperature is set to 1000 degrees Kelvin. Change this to estimate BD17's temperature to within a few hundred degrees.
- The "COBE" sheet contains the Cosmic Microwave Background spectrum, measured by the Far Infrared Absolute Spectrophotometer (FIRAS) instrument on the Cosmic Background Explorer (COBE) mission. Is the temperature of 1000 K too hot or too cold? How accurately can you measure the temperature? Note on this sheet you have a second plot, which shows the difference between the measured flux and the black body spectrum at your temperature. We also plot the uncertainty in the measurements. As you get close to the correct temperature, the errors are much larger than the differences. To make things show up on the plot well, you can reduce the size of the error bars by changing the uncertainty factor. The plotted uncertainty is divided by the uncertainty factor, so use a number like 10 or 100 or 1000 as you get close to the correct temperature. Can you get with 0.1 degrees? 0.01?