Getting to Higgs

Making a Histogram - An Example

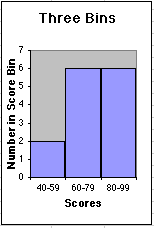
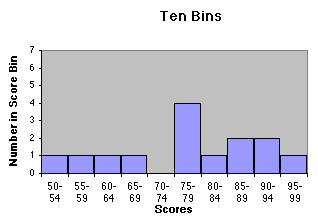
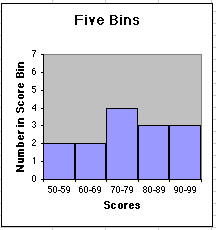
The teacher grades the tests and creates bins of width 10 points: . . . , 30-39, 40-49, 50-59, 60-69, 70-79, . . . . The number of test scores in each data bin is recorded and plotted as a bar graph.

Data
Student	Grade
Bullwinkle	84
Rocky	91
Bugs	75
Daffy	68
Wylie	98
Mickey	78
Minnie	77
Lucy	86
Linus	94
Asterix	64
Obelix	59
Donald	54
Sam	89
Taz	76

Miss Chang's Physics class has just taken a test. In order to come up with meaningful grades, Miss Chang will make a histogram to represent the distribution of grades and find a reasonable central value.

The critical question is that of bin size. Clearly, a bin size of 100 makes no sense as it puts all the data in one bin, giving us no information. At the same time, a bin size of 1 or less makes no sense, as the bins would be so small as to look pretty much like a simple list of results. We already have that!

Let's try a few bin sizes:

bin width of 20
bin width of 3
bin width of 10

This makes it sound like 10 is the best width. Actually, we don't know that. First of all, 8 or 12 might be better. Secondly, narrower or wider bins might give us the look at the data that we need in a particular case.

To more easily see how the size of the bin affects the shape of the curve, try the dynamic histogram.

References

Assignments: Identifying B - Identifying W